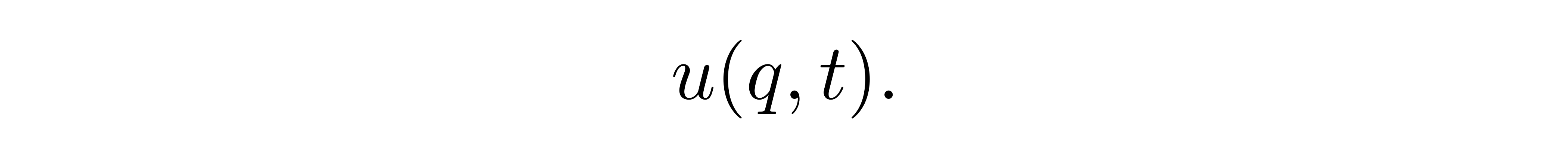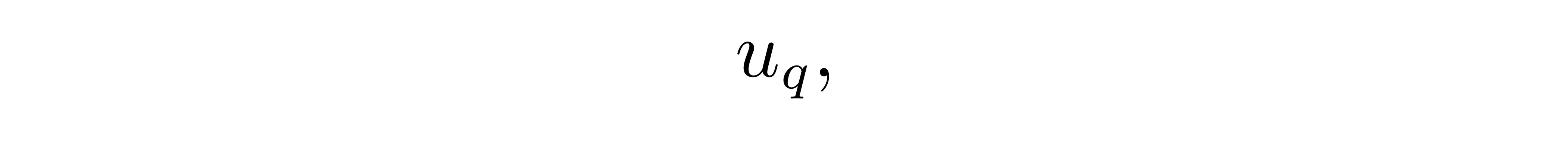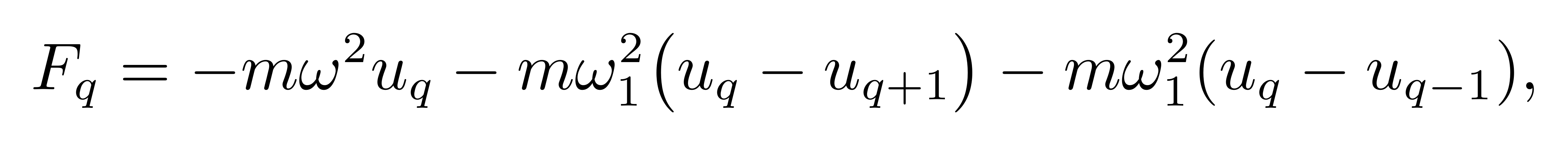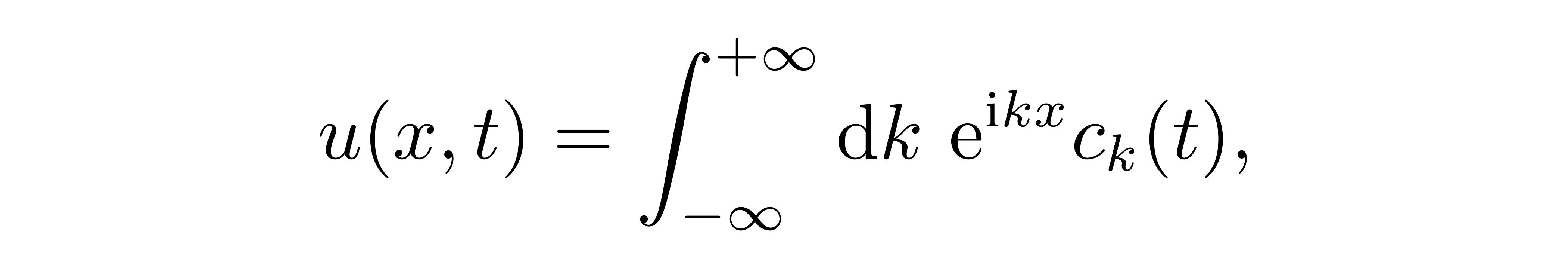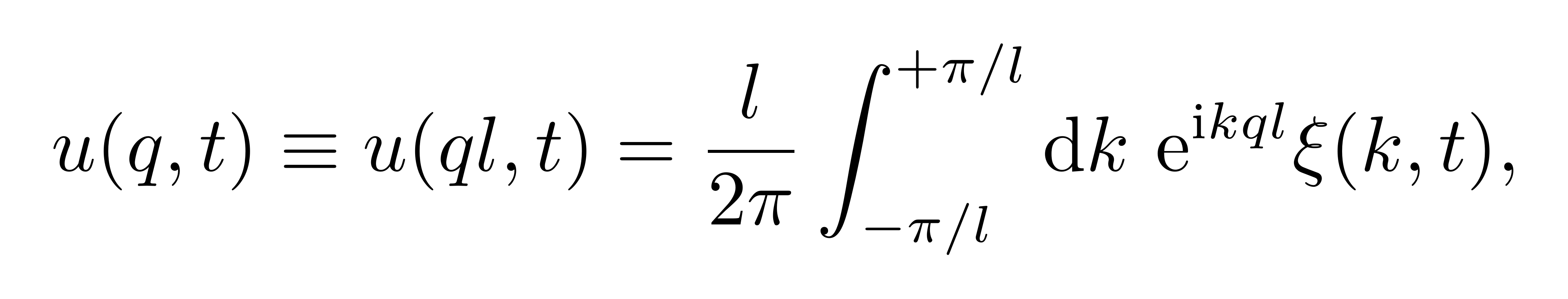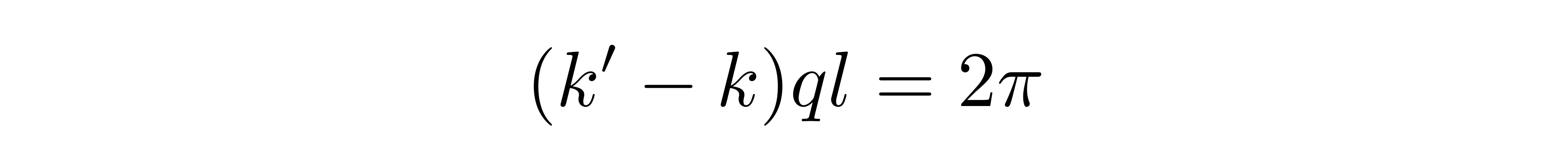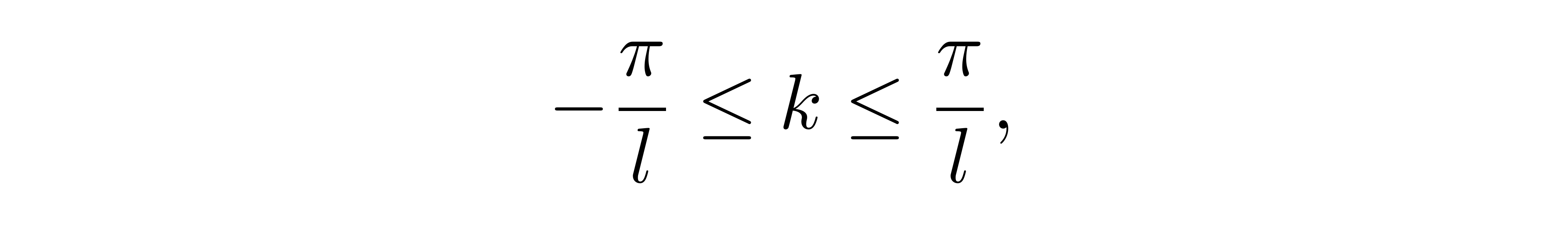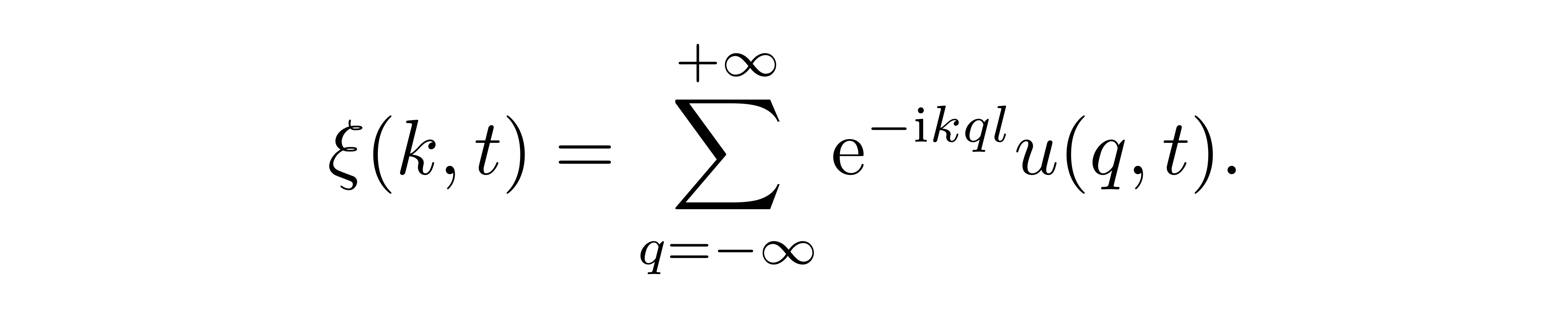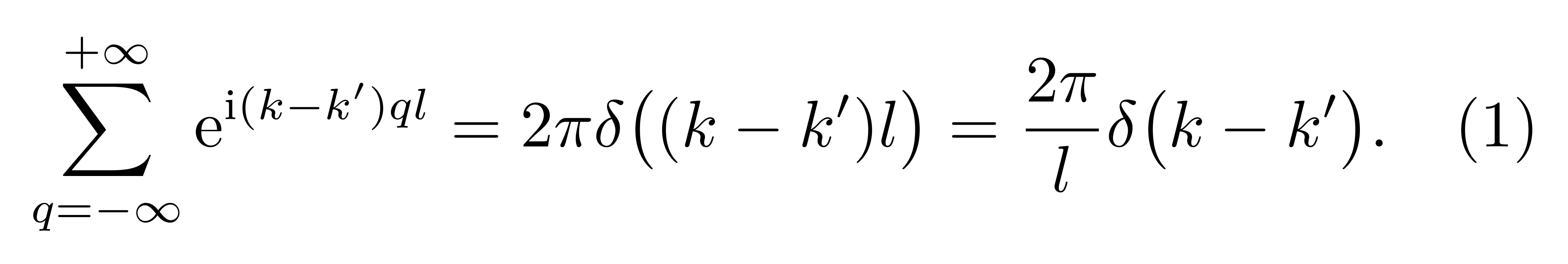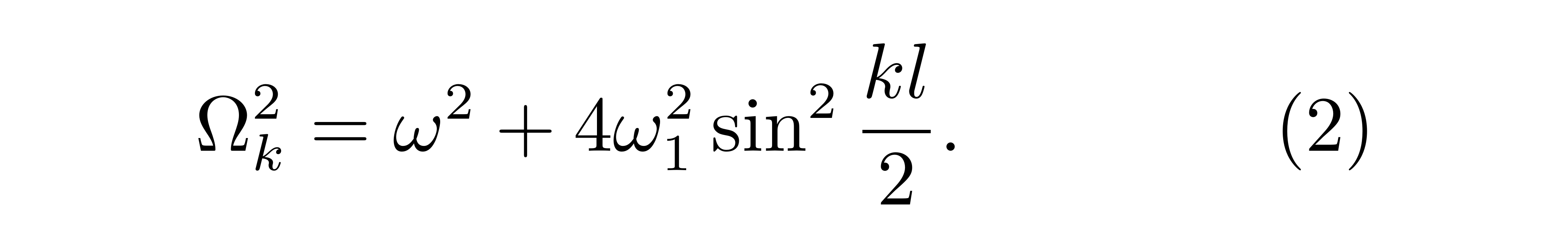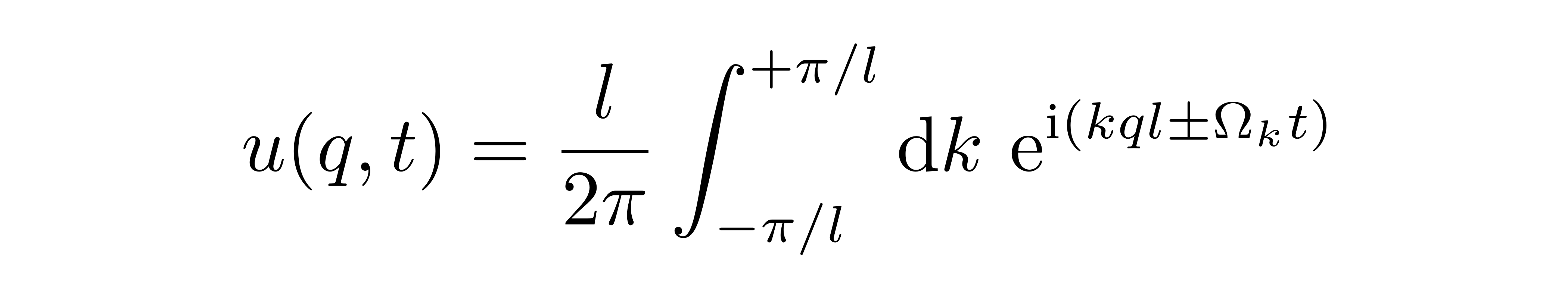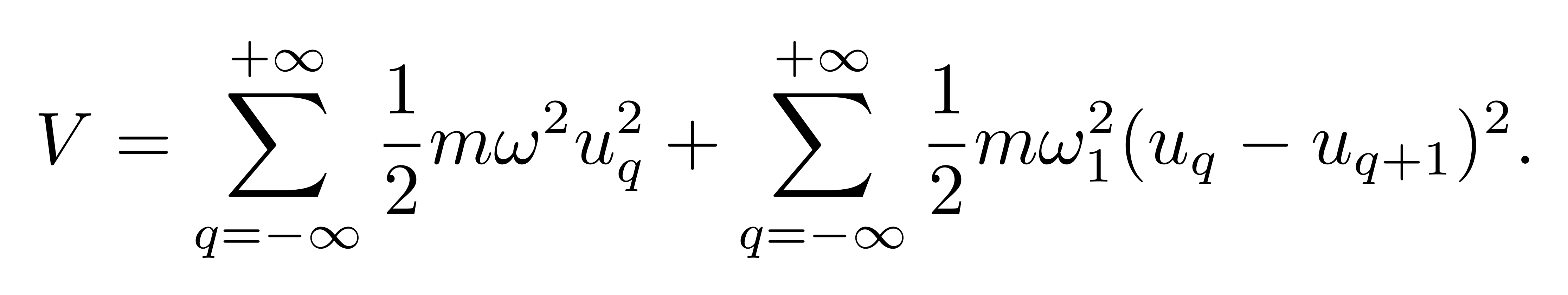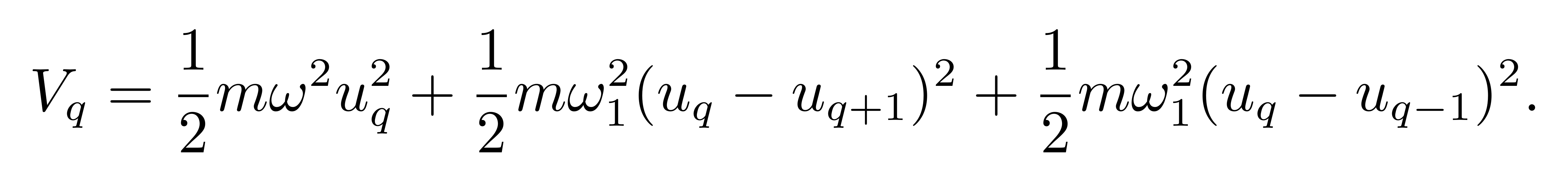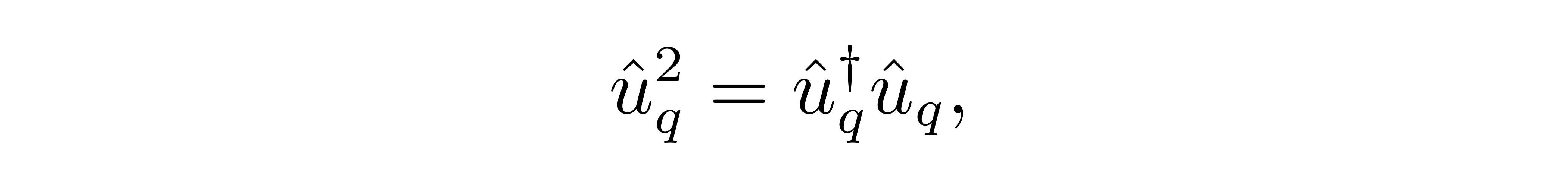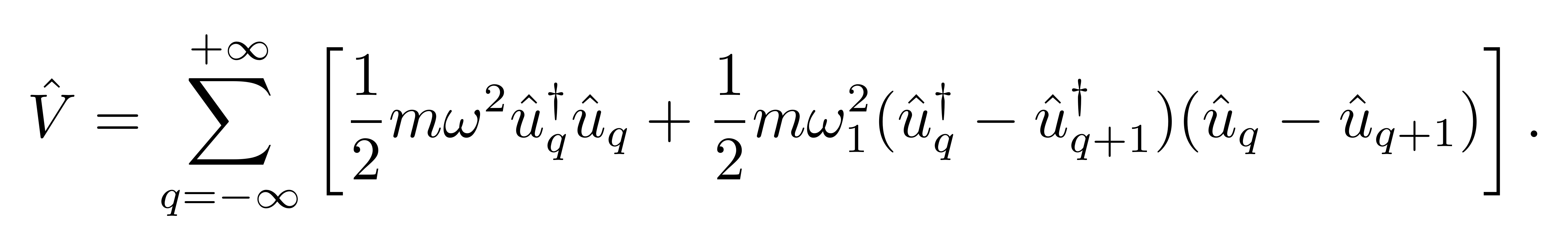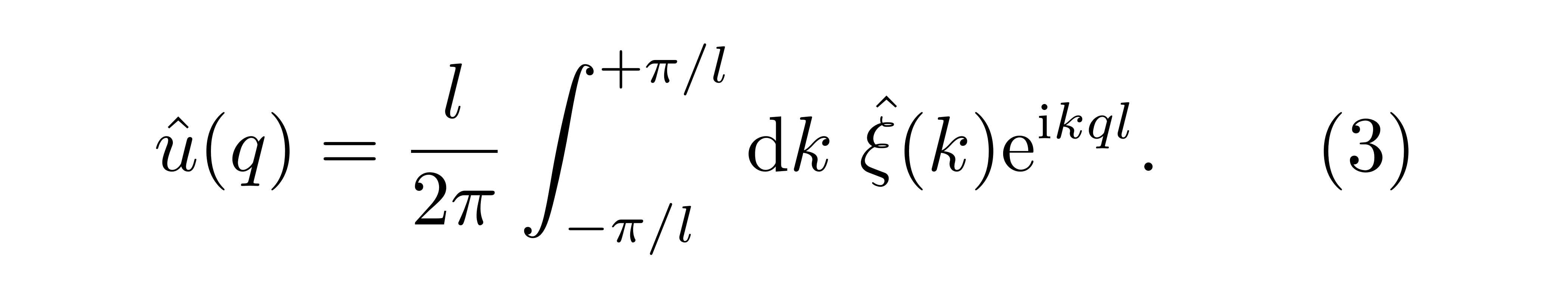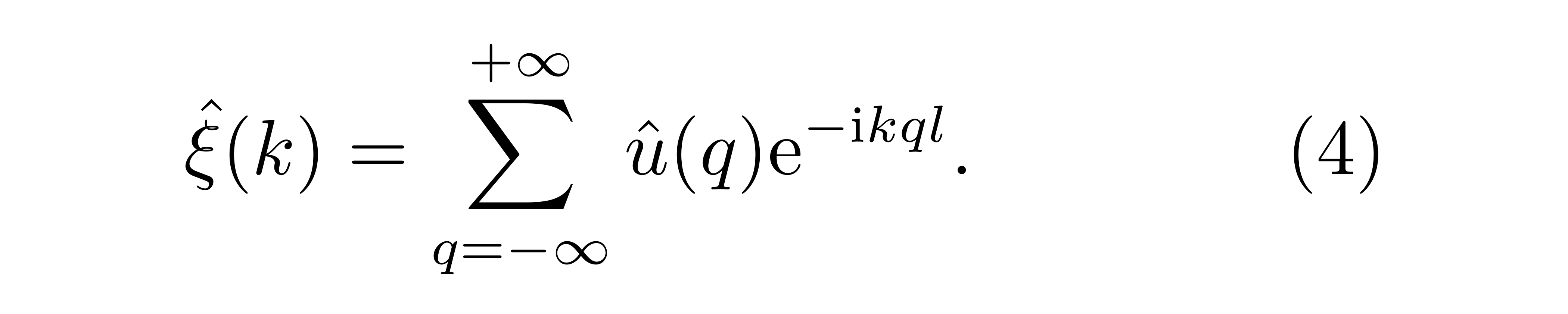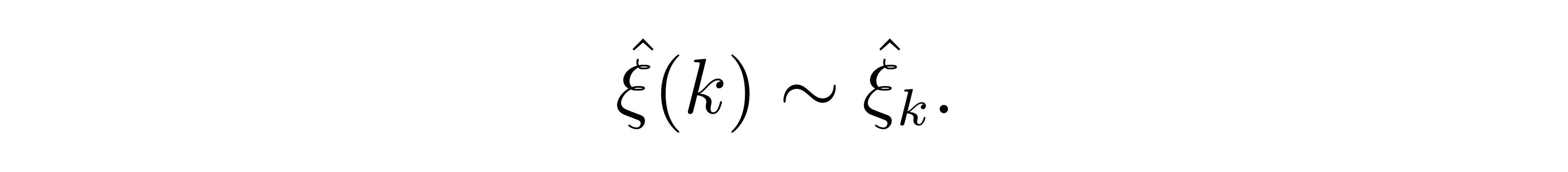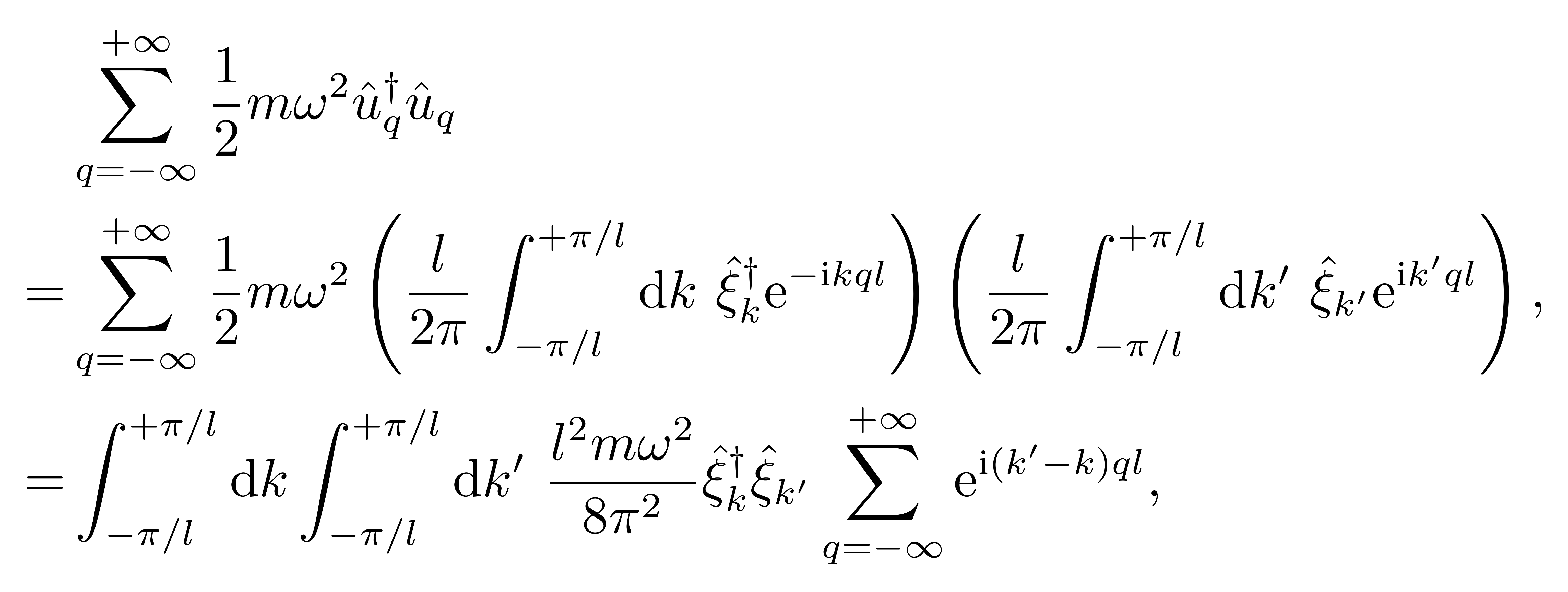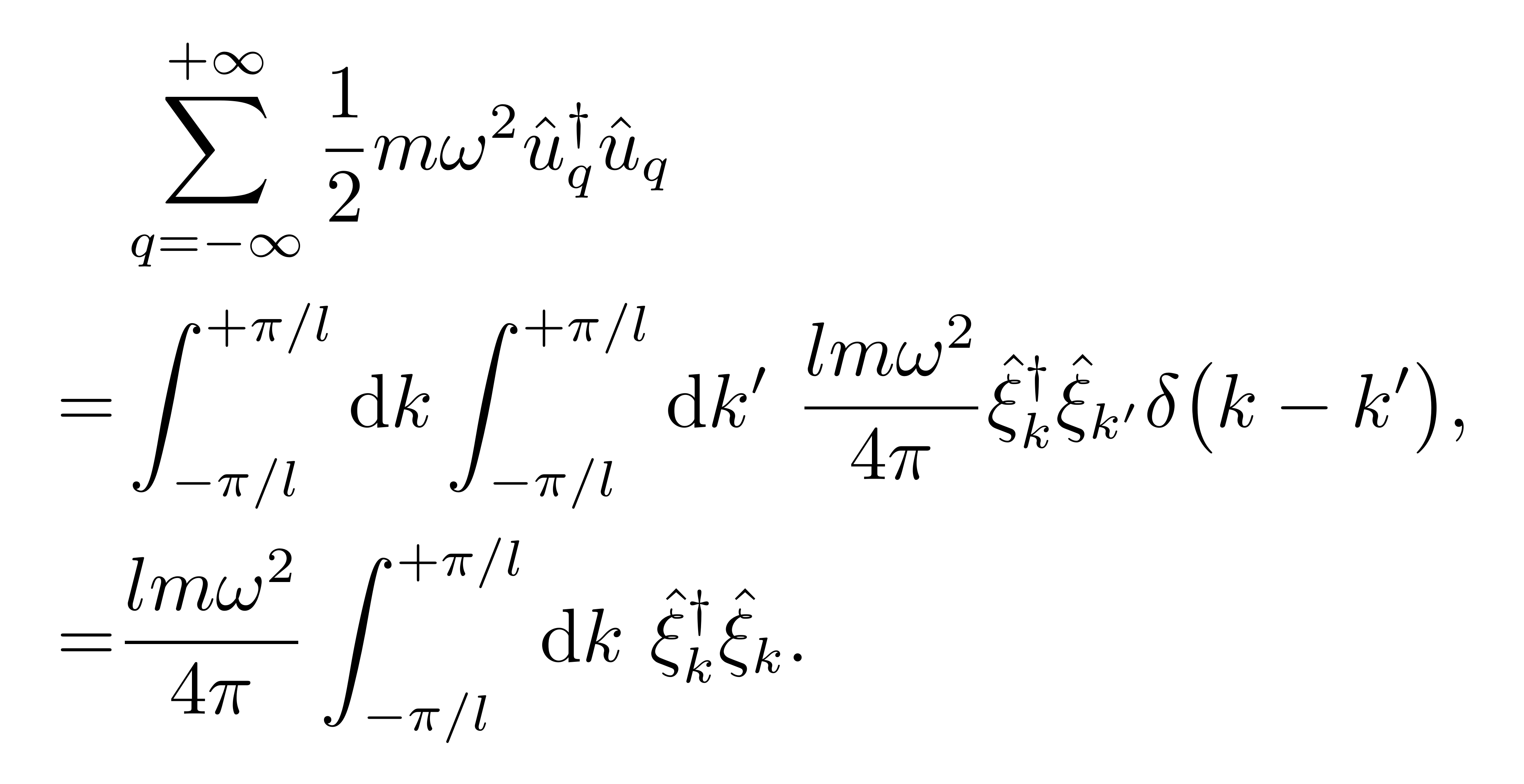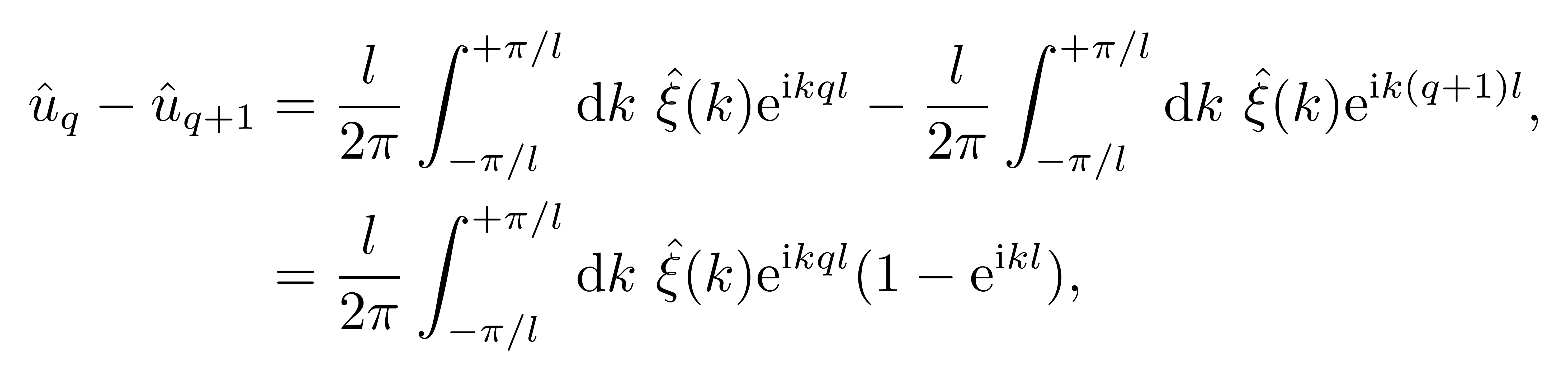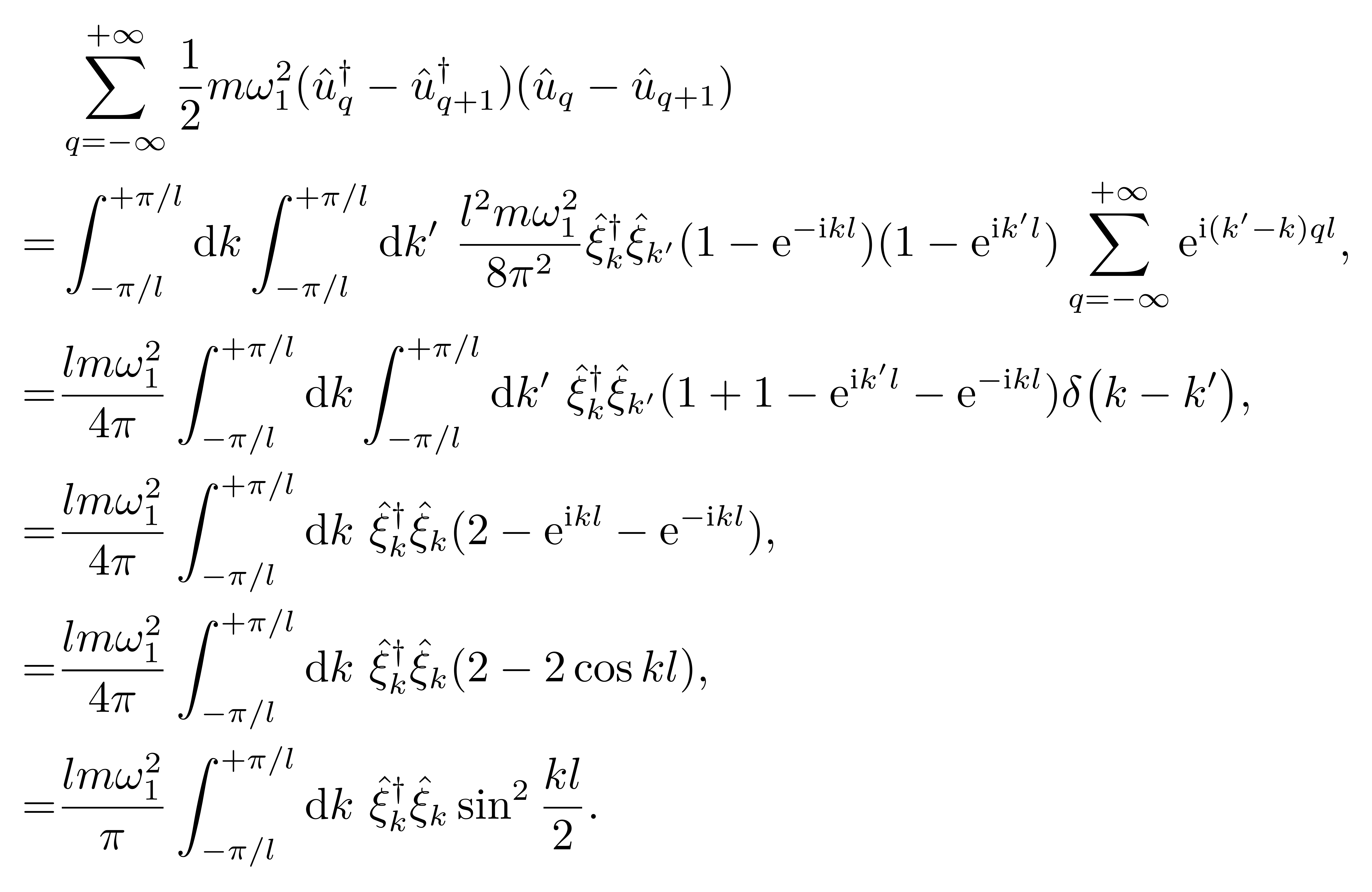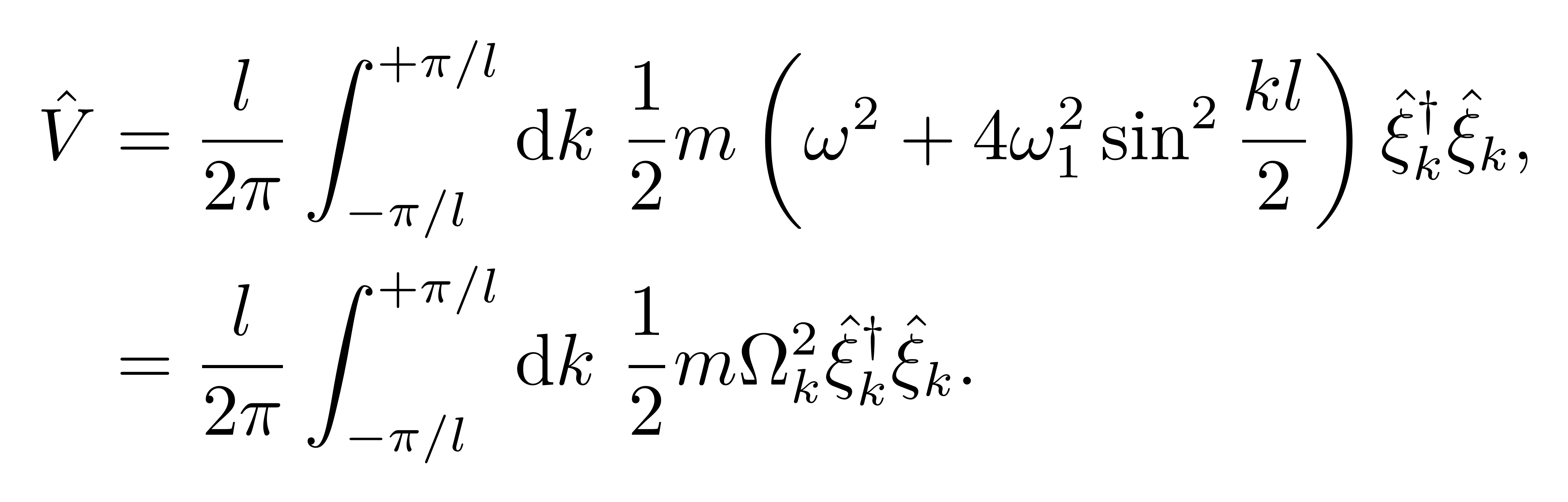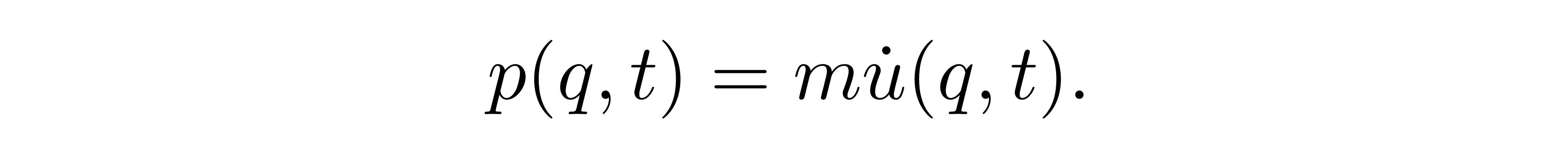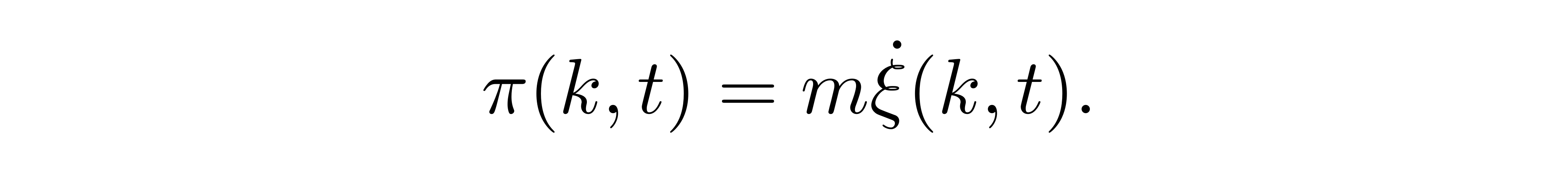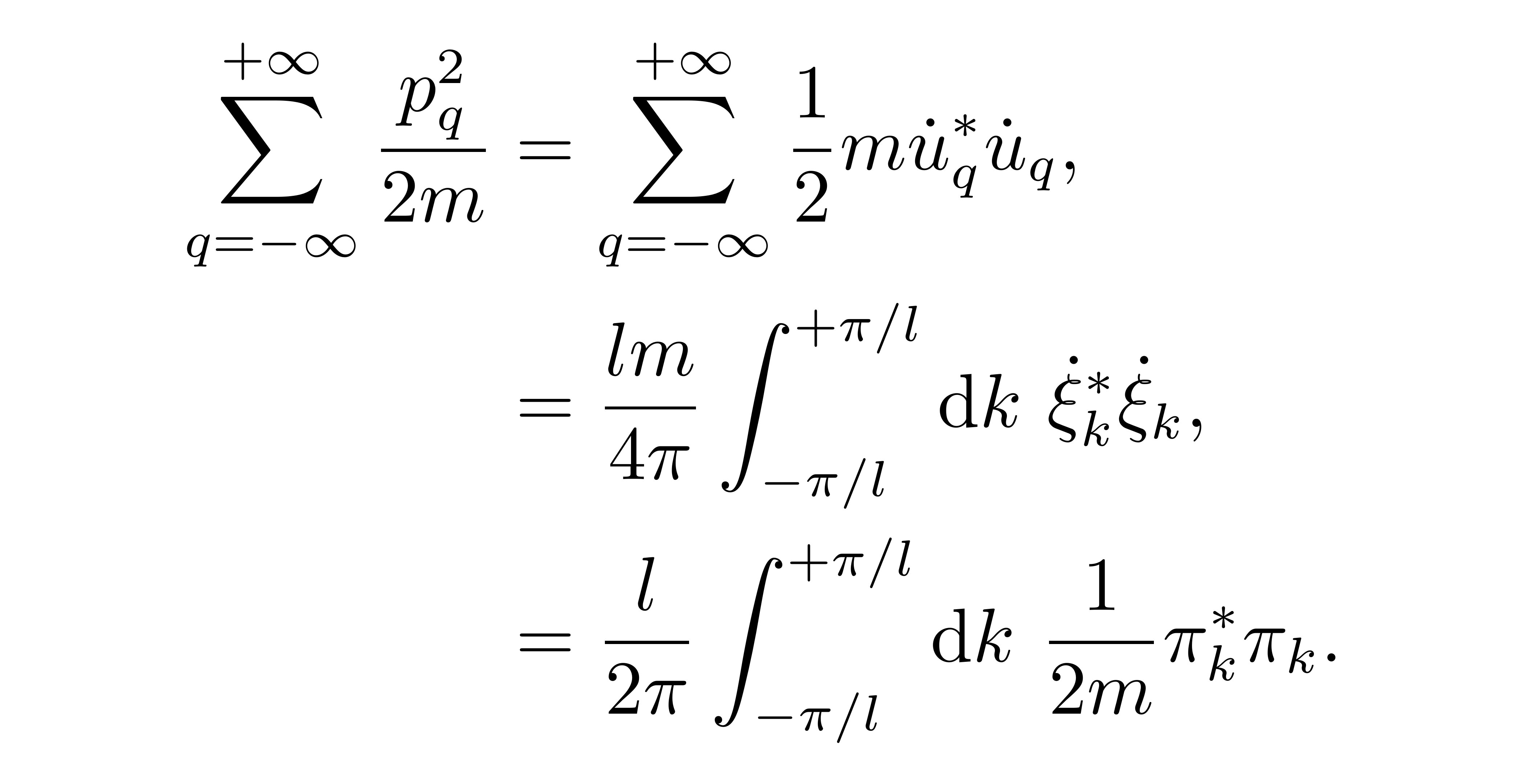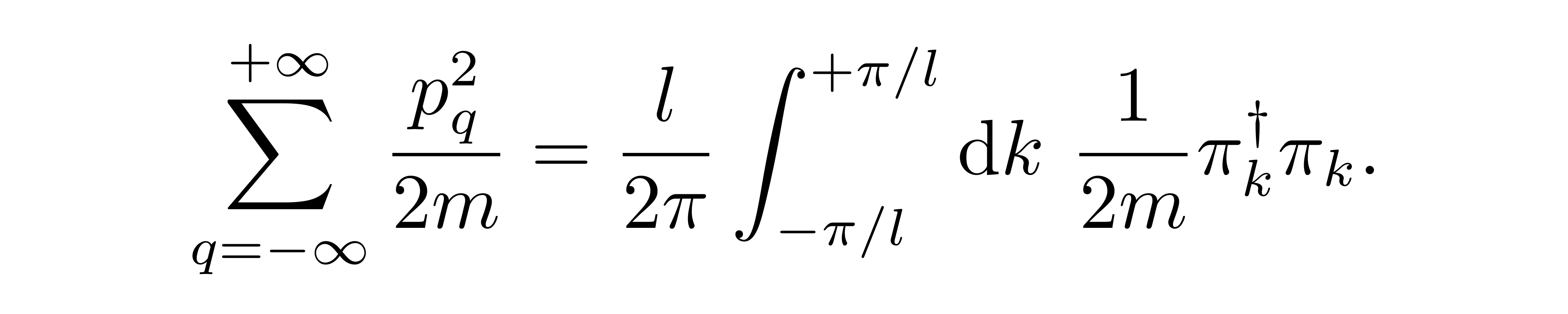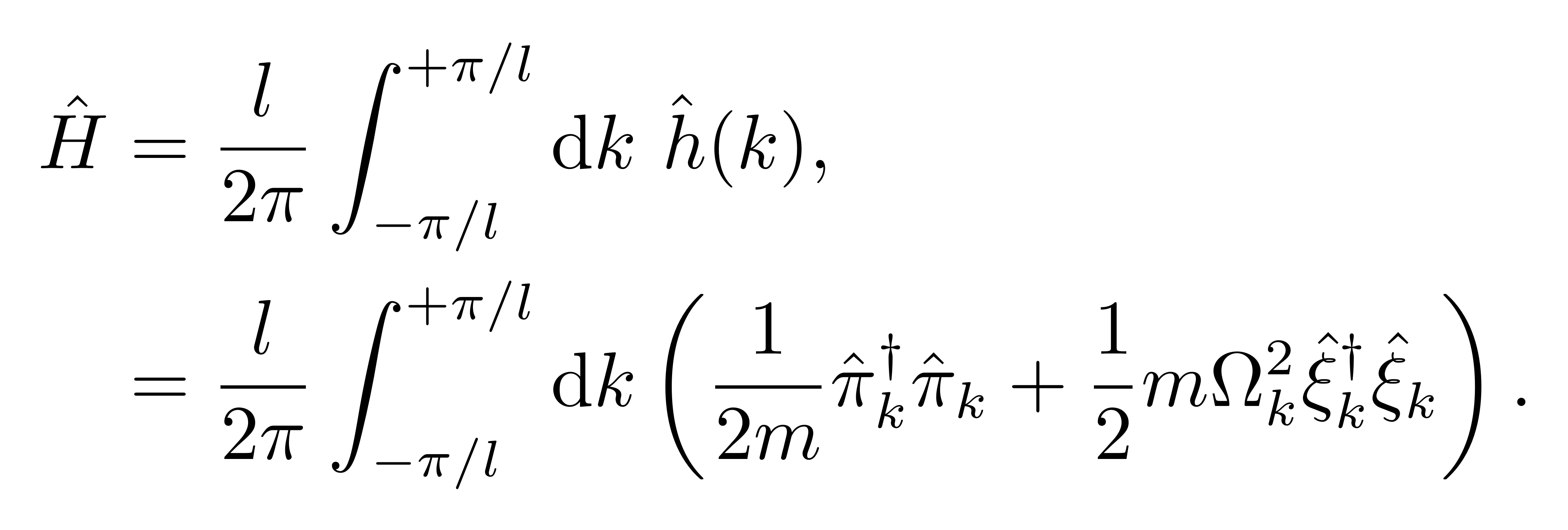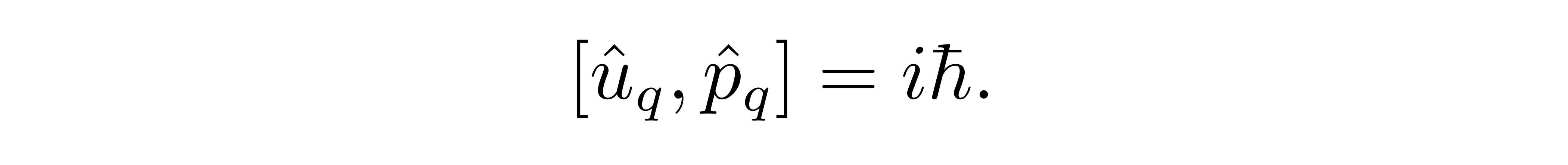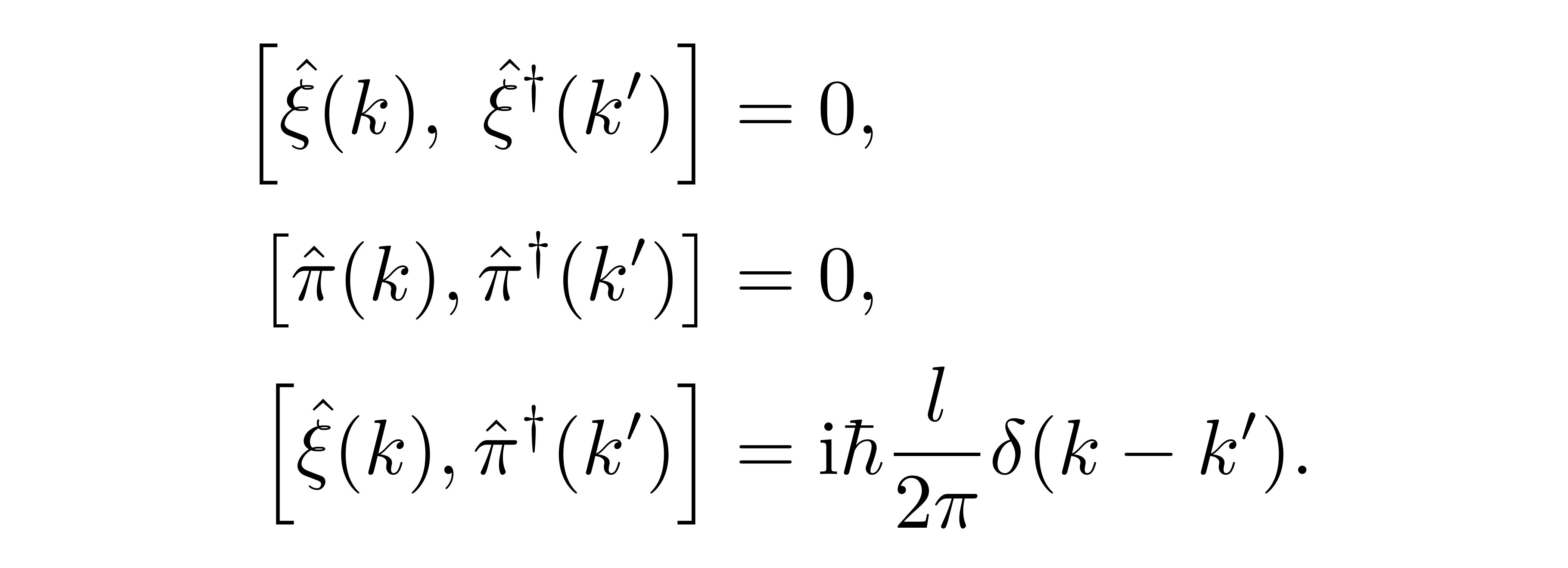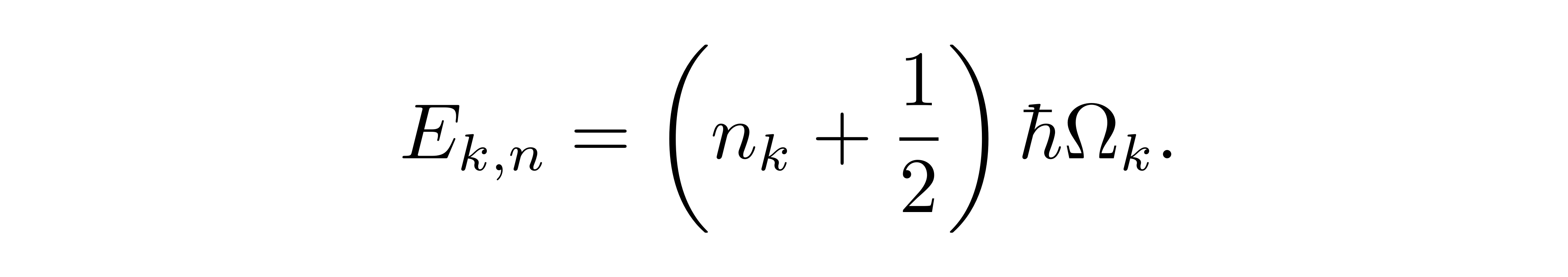This guide will guide you on how to profit from your blog. If you need guidance on how to start a blog we recommend reading our Step by Step How to start a blog guide. Blog owners with 10,000 to 100,000 monthly page views often earn between 2 cents and 10 cents for each page view from advertising, equating to $200 to $10,000 per month. Sponsored articles range in price from $25 to $750 for each post, depending on the size of the audience, genre, and individual sponsorship agreement.
Penalty to be missed Look in particular for local team news where the regular striker or penalty taker is out for whatever reason.
football bet
The example is Spurs (-1. If you bet on Spurs, they must win by two goals for the bet to win
其后,张朝阳发现,可以借鉴同样的思路来处理一维量子谐振子链。引入算符的格点傅里叶变换后,他成功地在“k空间”将哈密顿量算符重写为若干个不同频率的谐振子的哈密顿量算符之和。对给定频率的谐振子,我们总能相应地定义其升降算符,它们的作用结果是引起一个单位能量的增减,由此带来“声子”产生和湮灭这一物理图像。在固体物理和凝聚态物理中,“声子”即对应晶格的某个集体激发模式。

一维谐振子链上的经典格波
从一、到二、到无穷,在上节课程中,张朝阳仔细讨论了等间距排列在 x 轴上的无穷多个经典谐振子体系(如图)的动力学行为。
![]()
这样一个体系又被称为一个经典谐振子链,或者是一个格点(Lattice)谐振子体系。如果体系保持静止时,链上的每一个谐振子将静止在它的平衡点 x = ql 处,其中 l 为格点间间距, q 为任意整数,可以作为链上各谐振子的标记。如果在某一时刻受到扰动,链上的谐振子可能会偏移平衡点一段距离,这个距离可以统一地记为
![]()
为了书写简便,在不引起混淆时,下面讨论中我们一般也将其简记为
![]()
暂时地忽视其对时间的依赖关系。
一维谐振子链动力学即是研究这样一个二元函数随时间的演化行为。在牛顿力学的框架下,以第 q 个谐振子会同时受到一个将其束缚在平衡点附近的向心力,以及相邻格点 (q ± 1)上两谐振子对它的张力。在谐振子链的模型中,它们都具有弹力的形式
![]()
再利用牛顿第二定律即可相应地给出链上各谐振子的运动方程。乍看之下,这样一个体系的动力学方程似乎过于复杂甚至于是不可解的。但张朝阳指出,对二体谐振子和弦振动的讨论给予了我们很好的启发:前者告诉我们可以通过组合变量将耦合的谐振子分解为若干个自由的谐振子;而后者告诉我们傅里叶分析是模式分解常用的数学工具。
于是仿照波动力学中的傅里叶分解
![]()
取第一个变量为离散化的坐标,有
![]()
称之为格点傅里叶变换。值得注意的是,在格点傅里叶变换中,积分区域并不能取到整个实轴,而是被固定在一个有限长度的区间内。这是因为当 q 取为整数,而两个参数 k 和 k' 的取值满足
![]()
时,对应指数部分取值相同,即其代表的事实上是同一个波形。于是,为了在分解中不重复计数,我们将参数取值限定到 k 的一个周期之内,不妨取为
![]()
即得到相应的积分区域。同时,可以考虑取格点上的逆傅里叶变换,有
![]()
具体的计算过程在上一节过程中已经展开过详细的讨论,这里不再赘述。张朝阳强调,其关键在于利用求和关系
![]()
在下面的讨论中,我们也将反复地、但暂不加证明地用到这一关系,以化简我们所得的结果。
将格点傅里叶展开代入运动方程中,不难发现傅里叶变换将谐振子链的集体振荡分解为了若干个自由振荡模式。其中每个自由振荡模式将满足一个经典谐振子方程,对应振荡频率
![]()
依赖于参数 k,又称其为色散关系。在色散关系中,我们也可以注意到参数 k 取值的周期关系,这与前面的分析是一致的。如果从关注单一谐振子的运动转向关注谐振子链的集体行为,不难发现每一模式都对应形成一个沿链条传播的类正弦波动,而其叠加的结果
![]()
也可以被解释为是某一在链条上传播的波,习惯上称之为“格波”,即“在格点上的波动”,以区分在譬如一根弦或者空气水体等连续介质上的波动现象。对格波可以作这样的想象,如图,独立地看时格点上每一点都在各自偏离平衡位置(红色圈)上下运动,而从整个链条的角度——如果用一条虚线将这些点连起来——它们即形成一个波。
![]()
特别地,如果各点上振动的频率保持一致时,整个链条上观察到的波动应该具有类正弦波的波形,此即我们所分解出的某一简正模式。
![]() (张朝阳介绍一维经典谐振子链上的格波)
(张朝阳介绍一维经典谐振子链上的格波)
一维谐振子链的量子化及模式分解
对经典的谐振子链作了充分的讨论后,张朝阳转而关心如果链条上每一点处所放置的不是一个经典的谐振子,而是量子的谐振子时,整个体系又该如何运动和演化呢?着手处理一个量子体系时,我们一般的思路是先问其经典哈密顿量是什么,再选择合适的自由度将其算符化。
首先讨论一个一维谐振子链对应的哈密顿量。先看势能部分,仍然取偏移量 u(q,t) 为自由度,发生偏移时,整个链条具有势能
![]()
这里张朝阳提醒与上一节课中,链条中某一谐振子自身所感受到的势场
![]()
进行对比与区分。从整个链条的角度,相邻谐振子间的作用是相互的,它们之间只贡献一个相应的势能,不应该重复计算。作量子化时,需要将对应的自由度取为算符
![]()
需要注意地是,在算符化后,力学量算符不再函数,而值依赖于参数 k。为了后面叙述简便,我们对出现平方项改写为
![]()
于是有势能算符
![]()
对经典谐振子链的讨论启发我们,应该考虑对偏移量作傅里叶变换,以期寻找到独立的集体激发的简正模式。类比经典谐振子链,对算符取格点傅里叶变换后有
![]()
或者其逆形式
![]()
注意到,不同于 u,此时在“ k 空间”上定义的函数 ξ 应该是个复函数。在不引起混淆时,下面讨论中我们同样简记
![]()
将傅里叶展开 (3) 代入势能中的第一项,有
![]()
再利用恒等关系 (1) ,可以得到
![]()
而利用
![]()
可以类似地将势能算符中的第二项改写为
![]()
于是,整个势能算符可以表达为
![]()
另一方面,完整的哈密顿量还应当包括动能部分。首先从经典的谐振子链着手,注意到在“ q 空间”上,粒子动量地定义为
![]()
在“ k 空间”上,函数 ξ(k, t) 本身仍有长度的量纲,而傅里叶变换不涉及时间变量 t,所以自然得有 ξ 的共轭动量应当取为
![]()
事实上,利用傅里叶展开的形式不难验证其正确性。于是,动能项可以表达为
![]()
具体计算过程是类似与对势能项的分析,其中再一次用到了 u 的格点傅里叶展开,以及恒等关系 (1),这里不再赘述。再对应地取算符化,有
![]()
于是,可以把总的哈密顿量表达为
![]()
注意到,可以认为对给定每个参数 k,都有一组相应的、独立的哈密顿量(密度)h(k)。
同时,在量子力学中,我们还要讨论算符的对易关系。我们知道,在量子化的过程中,坐标和动量应当满足正则对易关系
![]()
利用该对应关系和逆格点傅里叶展开 (4),不难证明有
![]()
最后一个对应关系提出,当且仅当 k 与 k' 一致时,“坐标” ξ 与对应的“动量” π 不对易,且正则对易结果正比于 iℏ。这样一个对易关系,与相应的哈密顿量(密度)h(k) 的定义一齐提示我们,类似于经典谐振子的情形,一维量子谐振子链的哈密顿量也可以被分解为若干个以参数 k 标记的,独立振动的谐振子的叠加。每个独立谐振子分量有独立的振荡频率,或者说能级间隔,由色散关系 (2) 给出。回忆对单个谐振子的量子化,可以预期对每个给定的 k 模式,我们都可以通过组合 ξ 与 π 定义相应的升降算符,且预期可以给出相应的能谱
![]()
升降算符作用到某个态上,会在体系中提高或者减去一量子化的能量。类比光量子化,这样一个图景我们称之为升降算符产生或者湮灭一个能量为 ℏΩ_k 的声子。在固体物理或者凝聚态物理中,它可以用于描述晶格的振动模式或者说集体激发。相似的图像更可以被扩展到对自然界基本粒子的描述中,在我们建立认知和描述物质极其相互作用的理论中起到了举足轻重的作用,并带来了一系列的认知革命。
![]() (张朝阳推导一维谐振子链的哈密顿量算符)
(张朝阳推导一维谐振子链的哈密顿量算符)
据了解,《张朝阳的物理课》于每周五、周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
best app for sports betting
nj online casinos
online casino best payout
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。